|
|
Количество статьи: 297
Статьи за 24 часа: 0
[ Все статьи | Поиск | Top 10 | Категории ]
Морфология времени
|
«Я взглянул на вас, числа, и увидел вас одетыми в звери...»
Велимир Хлебников
Старые китайские художники называли изображение склонившегося под порывом ветра леса «телом ветра». Подобным образом можно назвать формы объектов природы «телами времени». Особенно это относится к таким объектам, как диссипативные структуры, - организованные потоки вещества и энергии. Тело времени – это форма инвариантная в течение этого времени. Поэтому эта форма может рассматриваться как форма самого времени. Ее уместно называть «хронотопом» (термин А.А. Ухтомского) или «овремененным пространством» (термин И. Пригожина). Содержание, существующее внутри этой формы, - это вещество, энергия или производные от них величины, которые являются содержанием законов физики. Все законы физики представляют собой вариационные принципы, которые описывают сохранение некоторого «содержания» в некотором «хронотопе». Это «содержание» мы и называем «физикой» в узком смысле слова, а хронотоп характеризует то, что обозначается термином «геометрия». «Физика» и «геометрия» дополнительны друг другу в отношении конкретного закона сохранения физики. Это значит, что один и тот же закон можно выразить простым содержанием в сложном хронотопе, а можно то же самое записать в виде сложного содержания в простом хронотопе. Примером такой дополнительности является Общая теория относительности. Существуют два ее варианта: первый, который создал А. Эйнштейн – это сложный хронотоп, в котором «содержание» - гравитационное поле - не обладает энергией, т.е. это «почти пустая оболочка», в которой существуют только инерциальные движения – очень простая физика. И есть альтернативный вариант этой теории - теория Логунова, где хронотоп простой, взятый из Специальной теории относительности, но содержание или физика сложные – там гравитационное поле обладает энергией.
Принцип дополнительности физики и геометрии последовательно развивал Габриэль Крон в своем методе описания электрических сетей.Он свел физику к простому закону Ома для участка цепи, а хронотоп сконструировал очень сложный при помощи многомерных тензоров, и динамика такой конструкции адекватно описывала процессы в сложных электрических сетях и машинах.
Существуют математические или общелогические корни такого понимания дополнительности физики и геометрии. В топологии есть теорема Роберта Герока о дополнительности логики и топологии: если в нектором процессе логического вывода наблюдается разрыв в логике или противоречие, то в более сложной топологии этого разрыва не будет – непрерывность логики восстанавливается. Если мы вместо «логики» возьмем «физику» (динамику), то получим искомый принцип: каждое явление можно описать либо сложной динамикой (физикой) в простом хронотопе, либо простой динамикой (физикой) в сложном хронотопе.
Для наглядности я запишу эту дополнительность в форме, напоминающей принцип Гейзенберга: ΔE Δt = const. Здесь изображена обратная пропорциональность сложности «содержания» ΔE (или «физики процесссов») и сложности хронотопа Δt (или «геометрии времени») данного явления. Эта запись – закон сохранения, описывающий некоторое явление. Каждый закон сохранения привязан к своему хронотопу.
В физике неживой природы хронотопы в основном несложные, поэтому физика до последнего времени не обращала внимания на проблему формы. Формы в физике рассматриваются скорее в качестве следствий или решений уравнений динамики. И только в таких явлениях, как высокотемпературная сверхпроводимость или физика искусственного термоядерного синтеза, проблема формы оказалась в центре внимания – только сложная адекватная форма организации хронотопа делает возможной саму физику этих явлений.
В физике живого состояния, напротив, проблема формы является центральной. Более того, можно сказать, что биофизика это наука о форме хронотопа. В организме нет никакой иной физики, нежели в неживой природе – это те же уравнения Ньютона, Максвелла, Ома или Навье-Стокса, но морфология хронотопа, в котором реализуется эта физика, очень сложна. В записи, приведенной выше, ΔЕ – это физика или динамика, а Δt – это биология или морфология процесса. Собственно вся биология без остатка сводится к изучению и описанию хронотопа Δt, т.е. морфологии. В.Н. Беклемишев говорил, что вся биология это и есть морфология. Так биология белков – это морфология катализа, биохимия – это морфология последовательных химических реакций, цитология – это морфология процессов переноса через мембраны, эмбриология – это морфология процесса деления клеток, эволюция – это морфология популяционной динамики (размножения) и т.д. Можно сказать, что морфология – это определение биологии с точки зрения физики.
Когда И.В. Гете вел яростную дискуссию с Ньютоном по поводу теории света, на заднем плане этого спора стояло совершенно особое понимание Гете значения формы, для которого не было места в физике того времени. Гете создал морфологию как науку, наметив тем самым место будущего моста между физикой и биологией. Но сам Гете стоял на плечах такого гиганта как Альбрехт Дюрер, который, видимо, первым осмыслил форму как характеристику самого пространства. В своей работе 1528 года он приводит изменение формы лица как следствие преобразования системы координат (рис.1). (Заметим, что это было сделано за сто лет до введения Декартом понятия о системе координат). В XVIII веке Гете использовал подобный подход в своей морфологии: он рассматривал разнообразие форм растений, как трансформацию формы исходного «прарастения» или архетипа. В ХХ веке д'Арси Томпсон наиболее последовательно изложил это понимание формы как пространства, в котором реализуется активность жизни. Рис.2 показывает его представление о том, как форма живых существ связана с кривизной пространства.
Все это прекрасно, скажет читатель, но при чем здесь время и хронотоп? Действительно, картинки Дюрера и д'Арси Томпсона касаются статики форм и о времени здесь речи нет. Но вспомним, что в начале ХХ века, когда д'Арси Томпсон рисовал свои картинки, Герман Минковский соединил пространство и время, придав времени смысл еще одной пространственной координаты. И это сразу превратило формы в хронотопы. Согласно Специальной теории относительности время движущегося объекта земедляется, а его форма искажается – сплющивается в направлении движения. Такую трансформацию формы можно изобразить эквивалентной трансформацией системы координат, которая называется «движением Пуанкаре» (Рис.15). 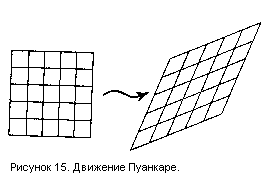
Соответственно форма объекта меняется приблизительно так, как это изобразил в свое время А. Дюрер (Рис.1). И мы имеем право сказать, что эти новые формы являются новыми хронотопами Специальной теории относительности. А формы д'Арси Томпсона (Рис.2) вполне эквивалентны искривленному пространству-времени Общей теории относительности – здесь время течет вдоль кривых координатных линий, а форма представляет собой инвариант этого течения и поэтому может быть рассматриваема как «тело времени» - его форма.
Вспомним, что мы говорили выше о двух вариантах Общей теории относительности Эйнштейна и Логунова и отнесем наши рассуждения к картинкам д'Арси Томпсона. Эти картинки представляют собой тот подход к описанию реальности, который избрал Эйнштейн: здесь «простая физика», которой соответствует изображение некоторого животного, трансформируется в «сложной геометрии» новой координатной системы. Тогда Логуновский подход должен заключаться в том, что мы рассматриваем «простую» прямоугольную систему координат, а трансформация формы животного является результатом изменения уравнений динамики, описывающей процессы, протекающие в этой системе координат. Последнее ближе к задаче описания времени – здесь уравнения описывают само течение времени, а форма животного, являющаяся решением этого уравнения, задает нам хронотоп.
Как должны выглядеть уравнения, описывающие течение времени? Когда-то Анри Бергсон сравнил течение времени с кинематографом: здесь время представляет собой итерационный процесс прибавления еще одного кадра «сейчас» к последовательности таких же кадров, ставших прошлым. Это линейный процесс итерации: xn+1 = xn + c («с» = сейчас), такой же линейный, как время в пространстве Минковского, что и позволяет изображать его как прямолинейную ось координат. Но в пространстве Общей теории относительности, как и на рисунках д'Арси Томпсона координаты криволинейны, поэтому для описания течения времени в таком пространстве нужно применять нелинейную итерацию. Простейшая из нелинейных итераций квадратичная: xn+1 = xn2 + c . Неожиданно исследование этой итерации в комплексной плоскости (т.е. когда числа «х» и «с» комплексные) привело в конце ХХ века к открытию целого мира форм – хронотопов. Это открытие сделал Бенуа Мандельброт.
Если в комплексной плоскости брать последовательно различные значения «с» и, исходя из х = 0, совершать с этим числом вышеприведенную квадратичную итерацию, то в результате это число либо станет бесконечно большим, либо устремится к нулю, в зависимости от исходного значения «с». Если закрашивать черным цветом те значения «с», которые в результате итерации не уходят на бесконечность, то в плоскости «с» мы обнаружим странную форму – инвариант квадратичной итерации – множество Мандельброта (Рис. 3). Это множество представляет собой хронотоп квадратичной итерации. Но этого мало – это множество представляет собой «библиотеку» иных хронотопов, которые называются множествами Жюлиа. Они тоже порождаются аналогичным образом той же самой квадратичной итерацией, но с фиксированным значением «с» и последовательным исследованием различных «х» на их способность уходить на бесконечность. Те «х», которые не уходят на бесконечность и образуют соответсвующее множество Жюлиа в плоскости «х». Некоторые из них показаны на Рис.3. вместе с указанием значений «с» на множестве Мандельброта, которым они соответствуют. Уже на этом рисунке видно, что множества Жюлиа очень напоминают некие органические формы. В 80-е годы К. Пикоувер исследовал формы множеств Жюлиа, порождаемые более сложными, чем квадратичная, нелинейными итерациями в комплексной плоскости, и обнаружил там формы, удивительно напоминающие микроорганизмы. Он назвал их «биоморфами» (Рис.5).
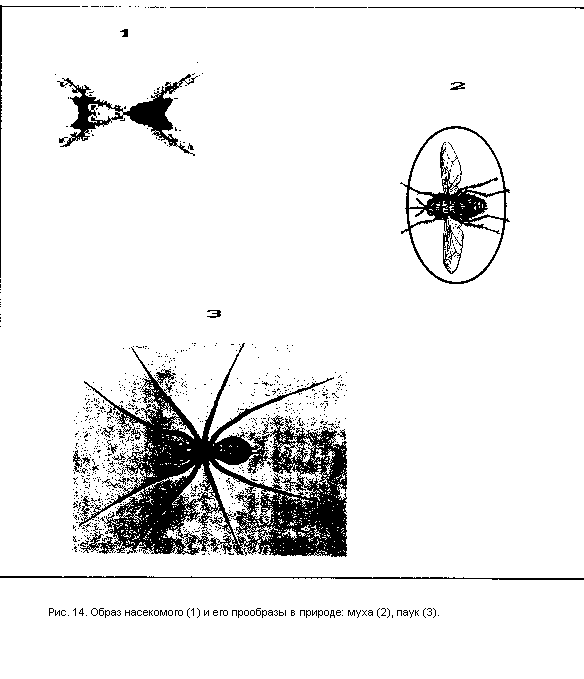
Биоморфы Пикоувера заставили меня задуматься над возможностью исследовать возможность получения трехмерных форм или хотя бы их двумерных сечений. Для этого я вместо комплексных чисел «х» взял кватернионы – гиперкомплексные числа с тремя мнимыми единицами. Эти «четырехмерные» числа придумал в начале ХIХ века У. Гамильтон, но они так и не пригодились физикам, которые предпочитали пользоваться трехмерными векторами. Но кватернионы, в отличие от векторов, это полноценные числа, которые позволяют производить над ними не только операции сложения, но и умножения и деления. Что мне и было нужно. Я создавал нелинейные комбинации из кватернионов, включая в них опреденное значение «с» из множества Мандельброта, и рассматривал получающиеся инвариантные формы – множества Жюлиа в плоскости дейсвительной и одной из мнимых осей кватерниона. Получившиеся «биоморфы» представлены на Рис.6-14. «Биоморфы» радиально симметричны относительно своей длинной оси – действительной оси кватерниона. Рядом с каждым «биоморфом» я поместил изображения реальных животных, форму которых он напоминает.
В чем смысл этой игры?
Во-первых, эта игра показала, что довольно сложные органические формы порождаются не очень сложными итерационными алгоритмами. При этом алгоритм играет роль «генотипа», а форма-хронотоп – роль «фенотипа» этих «животных». Причем понятию «генотип» возвращается его первоначальный смысл: автор термина «ген» В. Иогансен понимал его именно как алгоритм, управляющий образованием фенотипа. Я сконструировал два типа «генов», один из которых условно назвал «структурным геном», а второй – «регуляторным геном». Напомню, что в биологии структурные гены ответственны за синтез белков, из которых строится фенотип, а регуляторные гены определяют интенсивность синтеза тех или иных структурных генов. Мои «структурные гены» выглядят так: (q + c)n или qn + c ,где показатель «n» я брал в пределах от 2 до 5, «q» это кватернион, а «с» - это комплексное значение множества Мандельброта, для которого исследуется множество Жюлиа. «Регуляторный ген» - это алгоритм вида: (Aq2 + B)/(Fq + D) + с, где A, B, F, D – константы, «q» и «с» имеют тот же смысл, как и в «структурном гене». Этот алгоритм, как видно из его устройства, может, в зависимости от значения констант, как «растягивать», так и «сжимать» соответсвующее значение кватерниона, в то время как «структурный ген» только растягивает его. Отсюда и выбор таких названий. Путем комбинации нескольких «генов» одного и другого типа я составлял алгоритм итерации, порождающий «биоморфы», представленнные на Рис. 6-14.
Интересно, что путем усложнения «цепочки генов» удалось получить процесс «эмбриональной трансформации» (Рис.6): «бластула» получилась путем объединения двух «структурных генов», «ранняя гаструла» - путем объединения одного «регуляторного» и одного «структурного» из тех, что порождали «бластулу», «поздняя гаструла» была порождена объединением «регуляторного» и нового «структурного гена», нейрула была порождена объединением двух «структурных» и двух «регуляторных генов». Заметим, что весь этот «морфогенез» протекал в одной и той же области множества Мандельброта – я брал значение «с», соответствующее вершине «впадины» основной кардиоиды. «Взрослое животное», представленное на Рис.7, было порождено тем же алгоритмом, что и «нейрула», но для значения «с», взятого из области множества Мандельброта, где основная кардиоида соединяется с первой окружностью. Этот процесс «эмбриогенеза» раскрывает нам другой смысл проведенной игры – это понимание того, чем является множество Мандельброта для нашего познания и нашего мышления.
Как только не называли множество Мандельброта восторженные исследователи его красот. Большинство из них были охвачены мистическим чувством, когда погружаясь при помощи компьютера вглубь его границы, обнаруживали смутнознакомые органические формы. Это множество даже называли «Отпечатком пальца Бога». Я же полагаю, что Мандельброт открыл перед нами окно в космос идеальных форм Платона – космос эйдосов, которые организованы в виде древа, известного из Книги бытия как «древо жизни». Посмотрите на Рис.4 и вы увидите, как это древо, называемое здесь «древом бифуркаций», связано с множеством Мандельброта. Я обнаружил «эйдосы-биоморфы» на трех первых развилках этого «древа жизни» (в областях множества Мандельброта, соответствующих этим развилкам), включая его основание: основанию отвечают мои «эмбриональные формы» Рис.6, и биомормы Рис.9, Рис.12(2), Рис.14., первой развилке соответсвуют Рис.13, Рис.11 и Рис.7, второй развилке – Рис.8, Рис.10 и Рис.12(1). «Крону» этого древа я не исследовал – кто знает, какие «плоды» висят там?
Всвязи с «деревом бифуркаций» на Рис.4 уместно вспомнить два понятия, введенные в синергетике: «русло» и «джокер». Они примерно сооответсвуют понятиям траектория и точка бифуркации в математике. На Рис.4 ветви «дерева бифуркаций» изображают «русла», а развилки – «джокеры». Согласно современной нелинейной физике мир представляет собой хаос с островами порядка, т.е. огромное пространство «джокеров» с островами «русел». Время, как упорядоченную последовательность событий, можно обнаружить только в «руслах», причем русло может быть обратимым во времени, и тогда мы имеем в нем квазивремя механики - просто дление. А может быть необратимым (т.е. в «русло» проникают из сферы «джокера» хаотические влияния) и тогда это время термодинамики. А в самом «джокере» нет времени, в «джокере» можно перейти из одного времени-русла в другое время-русло. Законы физики существуют только в «руслах», - там мы можем записать вариационное уравнение и определить соответствующий закон сохранения. А в «джокере» нету закона – это область присутствия чуда, которое можно определить как событие смены законов. Можно сказать, что Бог творит в «джокере» новые «русла», каждое из которых это особый мир со своим хронотопом. Физика не случайно представляет собой набор почти не связанных между собой теорий – это теории о разных «руслах». Область «джокеров» – это не область физики, это область магии. До конца ХХ века физики считали, что реальность – это «русла», а «джокеры» в процессе познания превратятся в «русла», что приведет к научному овладению природой. В этом заключалась идеология материализма. Теперь похоже на то, что реальность – это «джокеры», а все «русла» – это острова не только в пространстве, но и во времени, т.е. это временные «русла», и время каждого из них когда-то кончается. Поэтому «русла» можно назвать виртуальными мирами. Бог творит эти миры из «джокеров», творит бытие «русел», но Сам не принадлежит ни к какому руслу, поэтому не обладает временным бытием. Бог, как творец бытия, не обладает бытием – эту аксиому сформулировал Дионисий Ареопагит еще в III веке н.э.
Т.о. мир предстанет перед нами как фрактал – самоподобный объект, который на каждом масштабе его рассмотрения представляет собой, как говорил Х.Л. Борхес «сад ветвящихся троп», состоящий из «русел» и соединяющих (разделяющих) их «джокеров». При этом на каждом уровне иерархии (масштабе расссмотрения) мы видим только «джокеры» этого уровня, а «джокеры» младшего уровня воспринимаются нами как часть «русла» старшего уровня. В математике существует такой объект, который называется «канторова пыль»: это фрактал, получающийся из отрезка прямой, из которого последовательно выбрасываются его части согласно опреденному правилу. В итоге бесконечной последовательности применения этой процедуры от отрезка остается бесконечное множество точек, суммарная длина которых (мера) равна нулю – это и есть «канторова пыль». Быть может и наш мир организован как канторова пыль - суммарная мера всех «русел» на всех уровнях иерархии равна нулю, а в действительности существуют только «джокеры», которые «прикидываюся» «руслами», когда на них смотришь с высоты иных уровней. Может быть физика – это иллюзия, которая поддерживается привязанностью нас, воспринимающих существ, к определнному масштабу реальности? А на самом деле реален только Бог, но мы в силу ограниченности нашего восприятия какие-то Его аспекты воспринимаем как физику, а какие-то как чудо. И то, что суммарная мера фрактальной реальности равна нулю как раз и отражает тот атрибут Бога, что Он не обладает бытием.
Если атрибутом Бога считать безвременье, то живое состояние, как носитель идеи Бога, приближается к этому свойству. С точки зрения времени живой организм – это попытка сведения времени к нулю. Термодинамически живое состояние – это диссипативная структура: это поток диссипации, т.е. рассеивания энтропии в среде, но поток нелинейный – в нем присутствуют обязательные обратные связи, которые в совокупности и составляют то, что мы называем организмом. И если поток диссипации мы отождествляем со временем, то обратные связи организма как раз это время локально (внутри организма) уничтожают. Вот примеры безвременья на разных уровнях организации: а) связанная вода, окружающая нативные белки: можно сказать, что это вода с измененной структурой, но можно сказать, что это вода с замедленным временем. Причем белок нативен только в таком временном окружении (при таком «минимуме времени»),б) в цепочках биохимических процессов реализуется т.н. принцип узкого места, или принцип «бутылочного горлышка», или «закон наименьших» А.А. Богданова – суть его в том, что скорость последовательности реакций определяется самой медленной реакцией, т.е. «минимумом времени», в) И.А. Аршавский еще в 60-е годы показал, что тренированный организм потребляет (и рассеивает) меньше энергии, чем нетренированный при выполнениии одной и той же работы. Т.е. чем полноценнее живое состояние организма, тем меньше времени через него протекает. Быть может, через святых время вообще не протекает, т.е. они достигли нуля времени – атрибута Бога. Это свойство минимума времени или замедления времени как раз и изображают мои «зверушки», ведь они образованы теми точками, которых время-итерация не уносит своим течением на бесконечность. И форма этих «зверушек» - это морфология безвременья, которая эквивалентна форме времени – это «тело времени» в смысле старых китайских мастеров. Интересно, что сами эти «зверушки» были обнаружены в областях безвременья – на развилках «древа бифуркаций» на Рис.4.
Резюмируя нашу прогулку по этому «саду ветвящихся троп», можно сказать, что множество Мандельброта – это дыра в «Платоновой пещере», где все мы пребывали до того дня, когда явился Мандельброт и обнаружил ее. И мы заглядываем в эту дыру при помощи наших компьютеров, чтобы рассмотреть детали мира эйдосов Платона. Мы уже обнаружили, что мир этот упорядочен как древо жизни. Это замечательно: наша приверженность древу познания, которой отличался наш ум еще в райском саду, сейчас принесла нам неожиданное открытие – оказалось, что древо познания и древо жизни это одно и то же древо. Именно оно организует наш мир в космос Платона.
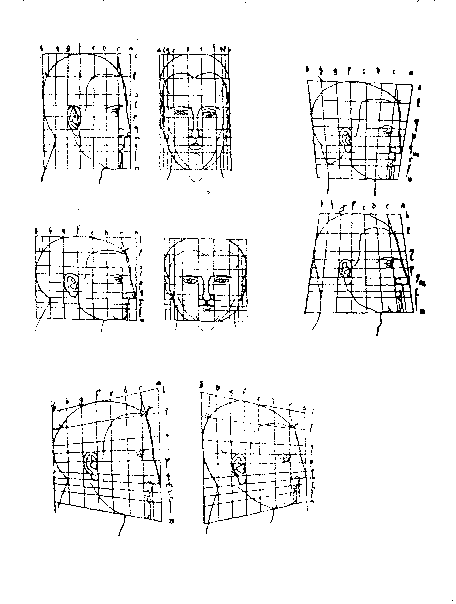
Рисунок 1. Изменение лица путем изменения системы координат по А. Дюреру (Эпштейн, 2003).
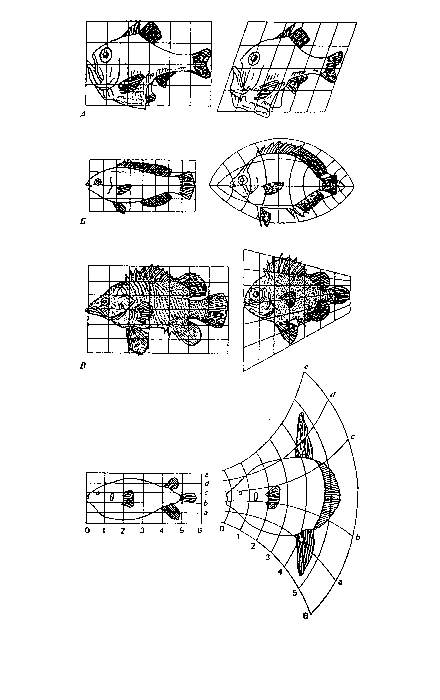
Рисунок 2. Изменение формы рыб путем изменения системы координат по д'Арси Томпсону (Эпштейн, 2003).

Рисунок 3. Множество Мандельброта с соответствующими отдельным его точкам множествами Жюлио (Пайтген, Рихтер, 1993)
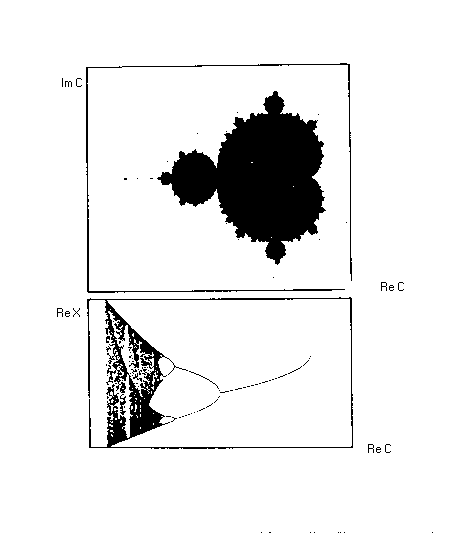
Рисунок 4. Соответствие между структурой множества Мандельброта в плоскости параметра с и структурой «дерева бифуркаций» для отображения xn+1 = x2n + c вдоль действительной оси с (Пайтген, Рихтер, 1993)
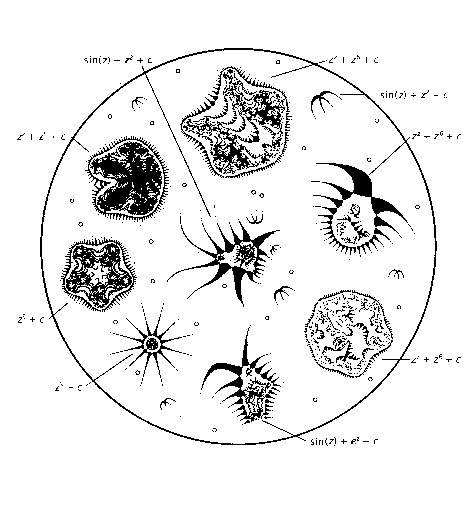
Рисунок 5. Биоморфы Пикоувера: каждому биоморфу соответствует своя порождающая его функция (В мире науки, 1989, №9).




 |
Дата: 15.10.2005, Просмотров: 5139
|
|
|

