|
«Вам повинуюсь, вас желаю, числа,
Незримые и легкие как тени,
Вы радугой связующей повисли
К сознанию с вершины мирозданья...»
Валерий Брюсов
По свидетельству Аристотеля, пифагорейцы считали, что «элементы чисел суть элементы всего существующего». Причем числа они наделяли вполне осязаемыми свойствами – формой, структурой. Они изображали числа упорядоченными фигурами из камушков. А их китайские коллеги точно так же рисовали числа состоящими из соответсвующего количества кружков: белых (четные) и черных (нечетные), соединенных линиями. На рис.1 вы можете видеть фигурные числа пифагорейцев:
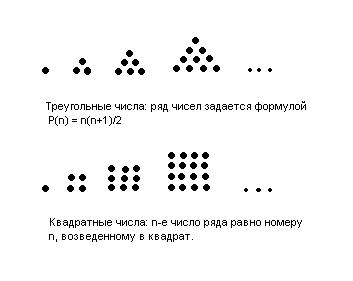
Рис.1. Фигурные числа.
Кроме плоских чисел существовали простанственные числа – пирамидальные, кубические и другие. Платоновы идеальные тела – правильные многогранники мыслились именно как формы чисел. Согласно Платону, такие фигурные числа занимают среднее положение между вещами и эйдосами. Не будет преувеличением сказать, что во времена Пифагора числа и были эйдосами. Математика в те времена еще не отделилась от нумерологии – геометризованной комбинаторики чисел. Интересно, что в Китае это нумерологическое направление в науке осталось доминирующим. Там оно называлось «сян шу чжи сюэ» - «учение о символах и числах». Эта теория символизационных пространственно-числовых структур лежит в основе гексаграмм «И цзин» - «Книги перемен». Пифагорейцы как и китайцы понимали числа как характеристики временных гармоний, поэтому рассматривали музыку как раздел математики. Древнегреческое arithmos «число» означает также «промежуток времени». На рис.1 под каждым рядом фигурных чисел приведен алгоритм их строения: если n отсчитывает время, то P(n) задает строение времени процесса т.е. его хронотоп. В греческой математике во времена Платона уже существовал раскол на логику и геометрию. Геометрия занималась статикой форм, логика занималась динамикой отношений этих форм. Именно последнее направление и стало содержанием европейской математики. По определению философа С.В. Чеснокова: «математика – это физика эйдосов». А нумерология, добавим мы, это геометрия эйдосов.
Почему греки стали относиться к числам так, как к ним относятся сейчас, т.е. чисто количественно? Может быть это связано с открытием пифагорейцами иррациональности числа √2? Непонятно было как изобразить форму такого числа. Аксиома Евдокса-Архимеда говорит о том, что между любыми двумя числами можно обнаружить еще одно число, а значит таких «монстров» среди них много, поэтому лучше отказаться от попыток их изображения. А вместе с ними постепенно отказались и от старой практики изображения фигурных чисел. Т.о. греки отказались от представления о форме времени, выражаемой числами. Но они любили формы и потому сосредоточили усилия своего интеллекта на статических формах геометрии и на физической статике. Так например Архимед умел интегрировать, но он понимал интеграл не как характеристику процесса, а как прием вычисления сложных статических форм. Только в ХVII веке с созданием анализа Ньютоном и Лейбницем математика вернулась к описанию процессов и их форм.
Но до этого существенно изменилось представление о числах. В Средние века появились отрицательные числа и нуль, т.е. у чисел появилась качественная характеристика «направление», имеющая два значения «плюс» и «минус». Числа образовали числовую ось, которая задавала образ течения времени:
←←←←←←0→→→→→→
где нуль соотвествовал событиям Священной истории, описанной в Евангелии. В ХVI веке при решении алгебраических уравнений появились мнимые числа, геометрическая интерпретация которых была дана в начале ХIХ века Ж. Арганом – у «направления» появилось еще два значения «плюс i» и «минус i». А вместе с ними бесконечное множество направлений (качеств) в комплексной плоскости. Основная теорема алгебры говорит о том, что все корни алгебраических уравнений находятся в комплексной плоскости. Т.е. множество алгебраических чисел отображается на множество комплексных чисел. Любые операции над комплексными (алгебраическими) числами не выводят нас за пределы комплексной плоскости. На рис.2 изображено комплексное число в эйлеровой форме z = a exp (iφ), где а – модуль, φ – аргумент числа. В этой записи явно выделены количественная характеристика числа «а» и качественная его характеристика «φ», задающая направление в плоскости А. Возведение комплексного числа в положительную действительную степень приводит к растяжению модуля и повороту аргумента против часовой стрелки. Последовательность таких операций возведения порождает логарифмическую спираль (рис.2).
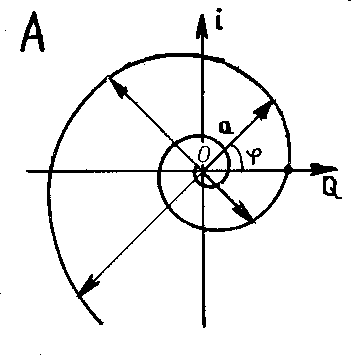
Рис.2. Логарифмическая спираль в комплексной плоскости А .
Если мы возьмем какое-либо число на действительной оси (Q на рис.2) и возведем его в комплексную степень, то получим некоторое комплексное число в плоскости А (возведение в мнимую степень – это поворот на некоторый угол). Т.е. операция возведения действительного числа в алгебраическую степень дает нам алгебраическое число: Q↑A = A (я здесь несколько произвольно отождествляю комплексные и алгебраические числа). Можно считать числа на действительной оси комплексными числами, аргумент которых кратен 2π для положительных чисел, и кратен π для отрицательных чисел. Тогда возведение такого числа в целую действительную степень дает снова число, лежащее на числовой оси: Q↑N = Q. Возведение же в дробную сепень дает число не совпадающее по направлению с числовой осью: Q↑R = A. В общем случае: Q↑Q = A.
«Спираль возведения» на рис.2 задает нам новый образ времени. При этом «линейное время» числовой оси, изображенное нами выше, теперь является частным случаем этого «времени плоскости» для случая возведения чисел действительной оси в целую сепень. «Спиральное время» очень распространено в природе, достаточно вспомнить раковины улиток:

Г. Кантор доказал, что множество всех алгебраических чисел счетно, откуда следует, что существуют и неалгебраические числа, поскольку уже действительные числа оси образуют множество мощности континуум. Неалгебраические числа стали называть трансцендентными числами. Где они расположены? – Всюду: почти вся числовая ось состоит из них, как установил Э. Борель. И комплексная плоскость в основном покрыта ими же – алгебраические числа в ней образуют «фрактальную пыль» в море трансцендентных чисел. Но исчерпывается ли множество трансцендентных чисел только комплексной плоскостью? В 1934 году А.О. Гельфонд доказал, что алгебраическое число в алгебраической иррациональной степени дает трансцендентное число: А↑А = Т. Мы говорили выше, что операция возведения в степень не может вывести комплексное число из комплексной плоскости. Ну а если каждое из этих алгебраических чисел принадлежит взаимноортогональным друг другу комплексным плоскостям? Возможно ли такое?
В ХIХ веке появились обобщения комплексных чисел на пространства размерности больше двух, так называемые гиперкомплексные числа - кватернионы У. Гамильтона и октавы А. Кэли. Пространство кватернионов содержит четыре взаимноортогональных оси – одну действительную и три мнимые: 1, i, j, k. Пространство чисел Кэли восьмимерно – одна действительная ось и семь мнимых: 1, i, j, k, l, m, p, s.
Мой учитель Д.В. Осадчий (о нем см. в эссе «Рассуждение о методе...») предложил следующий способ изображения кватернионов в трехмерном пространстве. Вообразим себе, что к концу вектора а на рис.2 приделан своим центром круг единичного радиуса, ортогональный плоскости А. Из центра этого круга восстановлены оси j и k (рис. 3). Теоретически они должны быть ортогональны как оси Q, так и оси i. Но в трехмерном пространстве это невозможно изобразить, поэтому на рис.3. только ось j ортогональна плоскости А, ось же k лежит в плоскости А.
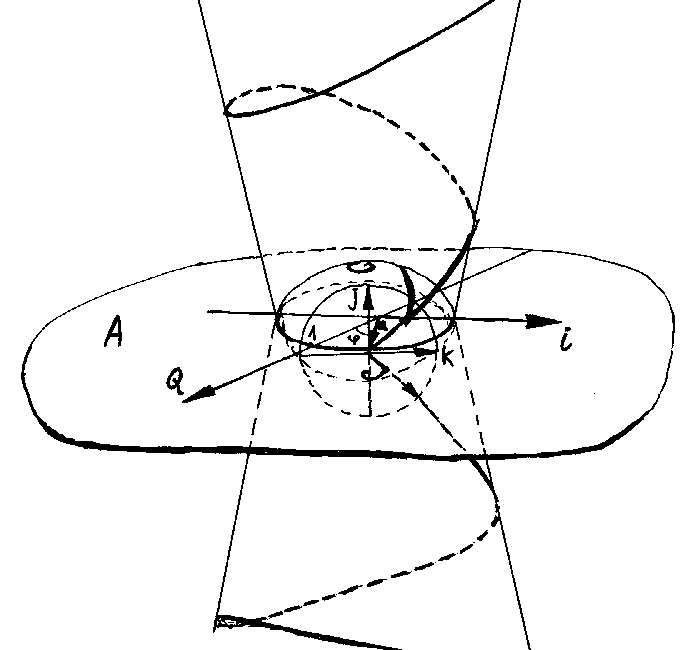
Рис.3. Возведение алгебраического числа в алгебраическую сепень по Д.В. Осадчему.
В единичной окружности (j,k) мы можем задать некоторое направление, не лежащее в плоскости А. На рис.3. показаны два таких направления (j,k) и (-j,k). Нужно иметь в виду, что спираль возведения в степень, изображенная на рис.2., находится и на плоскости А на рис.3. И новые направления возведения в сепень (с показателем больше единицы) на окружности (j,k) будут образовывать в трехмерном пространстве расширяющийся конус возведения в степень в случае, когда проекция нового направления возведения на плоскость А будет совпадать с направлением против часовой стрелки (см. рис.2). Причем это справедливо только для вектора а, модуль которого больше 1. Если же а < 1, то пространственная кривая возведения в степень образует спираль на «шапочке», изображенной на рис.3. Если проекция пространственного направления на плоскость А будет совпадать с направлением по часовой стрелке (см. рис.2) ( возведение в отрицательную степень с показателем больше единицы), то векторы по модулю больше единицы будут возводиться по скручивающейся спирали на «шапочке», а векторы по модулю меньше единицы будут возводиться по раскручивающейся спирали на конусе. Причем эти спирали будут противоположны по направлению вращения спиралям изображенным на рис.3. Два «конуса возведения» на рис.3, на которые расщепилась «спираль возведения» плоскости А (рис.2), образуют пространство возведения алгебраических чисел в алгебраическую степень, т.е. пространство трансцендентных чисел по Гельфонду. Если исходный вектор а единичный, то его пространственное возведение в степень происходит по поверхности, ограниченной кривой, называемой локсодромией (рис.4.).
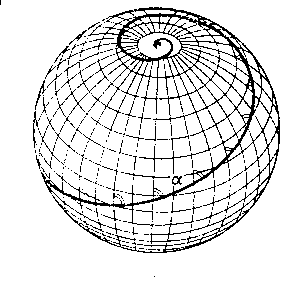
Рис.4. Локсодромия
На самом деле таких локсодромий на единичном «шаре возведения» много – в зависимости от направления исходного единичного вектора а, поэтому картина такого «шара возведения в степень» близка к той, что изобразил на своей гравюре Мауриц Эсхер (рис.6). С учетом этого «шар возведения» рис.3 превратится в рис.7. В действительности здесь нужно было бы вместо единичных «окружностей возведения» на конусах тоже изобразить единичные «шары возведения». Дело в том, что при перемножении направлений 1,i мы не выходим из плоскости единичной окружности (1i = i, ii = -1, -1i = -i, -ii = 1), а при перемножении направлений j,k единичный вектор движется по поверхности единичной сферы (ki = j, ji = -k, -ki = -j, -ji = k)(Рис.5).
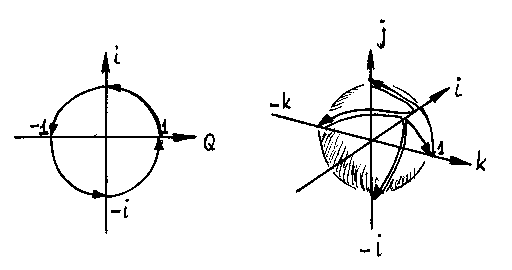
Рис.5. Единичная окружность возведения в комплексной плоскости (слева) и единичный шар возведения в пространстве кватернионов (справа).
На самом деле конусов возведения тоже должно быть много в зависимости от величины и напрвления исходного вектора и направления возведения в степень. Различные конусы возведения вложены друг в друга подобно листьям качана капусты. Т.е. вместо одной плоскости возведения на рис.2 в пространстве трансцендентных чисел мы имеем бесконечное множество поверхностей (конусов) возведения. Именно это обстоятельство объясняет почему кватернионы некоммутативны в отличие от комплексных чисел, т.е. для кватернионов справедливо соотношение АВ ≠ ВА. Мы уже говорили, что при перемножении комплесных чисел их модули перемножаются, а аргументы складываются. Вектор-произведение будет лежать в той же комплексной плоскости и направление его будет определяться суммой аргументов (углов поворота против часовой стрелки от действительной оси). В нашем пространстве кватернионов практически каждый кватернион лежит на своем конусе – на своем «листе капусты». Поэтому когда мы умножаем вектор А на вектор В, мы итоговый вектор АВ помещаем на конусе вектора А совершив вдоль спирали возведения на этом конусе поворот от вектора А, задаваемый аргументом вектора В. Когда же мы умножаем вектор В на вектор А, мы получаем равный по величине вектор ВА, но он уже лежит на конусе вектора В, относительно которого повернут на аргумент вектора А. Естественно, что в пространстве эти два вектора АВ и ВА не совпадают.

Рис.6. Гравюра Маурица Эсхера.
Это свойство некоммутативности заставляет вспомнить об операторах квантовой механики, которые еще называют q-числами в отличие от k-чисел классической механики. Оператор, или q-число, представляет собой дальнейшее развитие представления о качестве числа по пути от «направления числа» в комплексной плоскости к «форме числа» у пифагорейцев. Роль качества числа в операторах играет «собственная функция», которая превращает оператор в обычное k-число классической физики, которое называется в этом случае «собственным значением». Конусы возведения на рис.3 или рис.7 как раз и представляют собой собственные функции или качества (или формы) трансцендентных чисел – кватернионов. Наши картинки ведут нас к заключению, что объекты квантовой механики лежат на пространственных поверхностях в отличие от объектов классической механики, которые расположены на одной единственной плоскости.
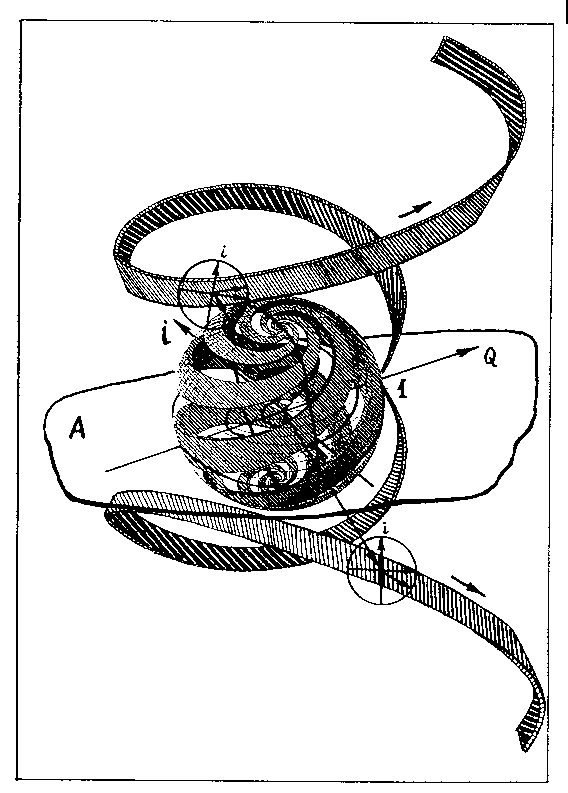
Рис.7. Пространство возведения алгебраических чисел в алгебраическую степень.
«Спиральное время» алгебраической плоскости теперь видится жалким остатком более разноообразного по своим формам пространственного времени или, точнее, пространственных времен. Эти времена играют роль «собственных функций» трансцендентных чисел. Алгебраическое уравнение можно рассматривать как дифференциальное уравнение, из которого «изгнано» время путем приравнивания нулю производной: dx/dt = 0. И.Ньютон считал, что пространство большей размерности образуется из пространства меньшей размерности при движении последнего в ортогональном ему направлении. Можно сказать, что производная описывает движение, которое превращает алгебраическое уравнение в дифференциальное. Согласно Г.В. Лейбницу интегрирование увеличивает число измерений. Он, а вслед за ним Л. Эйлер писали, что решение (интегрирование) дифференциальных уравнений требует выхода за пределы алгебраических величин и введения новых трансцендентных величин. Решение дифференциального уравнения можно рассматривать как некоторое многообразие, которое нечувствительно ко времени, задаваемому оператором дифференцирования. Это некий инвариант во времени. И такой инвариант имеет определенную форму – форму процесса, описываемого дифференциальным уравнением. Форма эта зависит как от вида дифференциального уравнения, так и от геометрии пространства переменных этого уравнения. Можно сказать, что здесь мы снова встречаемся с дополнительностью геометрии и динамики, о которой уже говорили выше. Сложность инвариантной формы может отражать сложность геометрии переменных при простоте уравнения динамики, но может отражать и сложность динамики при относительной простоте геометрии переменных. В качестве примера вспомним о множествах Жюлиа, описанных нами в эссе «Морфология времени». Там мы вместо непрерывного времени дифуравнений рассматривали дискретное время нелинейной итерации, беря в качестве переменных комплексные числа и кватернионы. Мы получили множество органических форм – биоморфов. Пример инвариантного множества в пространстве кватернионов приведен на рис.8.

Рис.8. Трехмерное множество Жюлиа в пространстве кватернионов (из книги Б. Мандельброта «Фрактальная геометрия природы»).
Напомню, что наши биоморфы получались благодаря комбинации итераций двух типов – нелинейной, которая «растягивала» значения переменной, и дробно-нелинейной, которая «сжимала» переменную. Такое «растяжение-сжатие», напоминает «преобразование пекаря» (раскатывание-складывание теста), о котором много писал И.Р. Пригожин. Идея дополнительности геометрии и динамики приводит к мысли, что еще более сложные числа, чем кватернионы, могут в своем бытии реализовать это «растяжение-сжатие», и тогда более простая динамика времени-итерации в пространстве этих чисел сможет порождать в качестве инвариантов сложные биоморфы.
Если А↑А = Т, точнее А↑А = Кв, где Кв – кватернион, то можно предположить, что Кв↑Кв = Ок, где Ок – октава, или число Кэли. Попробуем изобразить направление возведения в степень в пространстве чисел Кэли: 1, i, j, k, l, m, p, s (Рис. 9). Здесь каждый следующий «шар возведения» поворачивает исходный вектор в направлении ортогональном предыдущему «шару возведения». Т.о. в результате вектор, который возводился в степень против часовой стрелки (на рис.9 вверху), может быть возведен в степень против часовой стрелки в зависимости от величины аргумента в каждом из «шаров возведения».
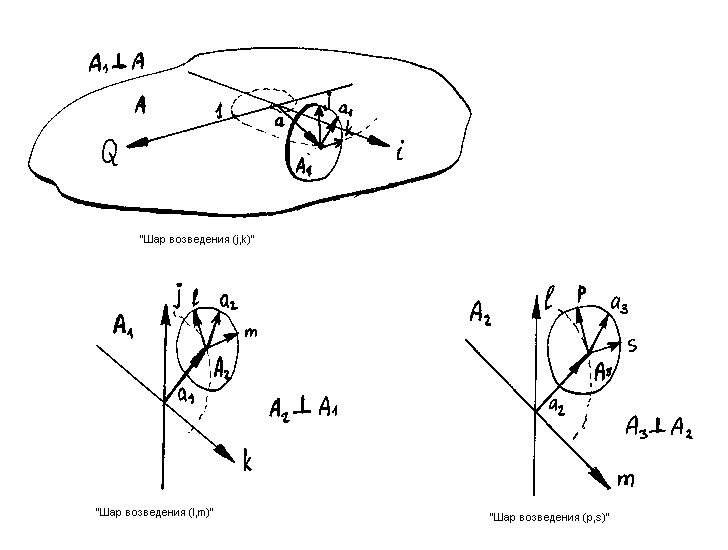
Рис.9. «Шары возведения» в пространстве октав.
Но если число росло в направлении против часовой стрелки, то оно будет уменьшаться в направлении по часовой стрелке. В результате мы получаем динамику растяжения-сжатия, которая зависит от значений отдельных компонент чисел Кэли, и в которую превращается обычная динамика возведения в степень – в пространстве кватернионов это было либо только растяжение, либо только сжатие (Рис. 10). Всилу этого «конусы возведения» в пространстве октав окажутся «смятыми» и «бесформенными». Согласно теореме Понтрягина (1931г.), «всякое локально компактное связное топологическое тело является либо полем действительных чисел, либо полем комплексных чисел, либо телом кватернионов». Следовательно топологическое тело, описываемое октавами, должно быть несвязным. Проявляется это в том, что в добавок к некомммутативности, у октав появляется свойство неассоциативности, т.е. А(ВС) ≠ (АВ)С. Т.е. в зависимости от того, какие «блоки» мы образуем (какую связность мы зададим), такой результат умножения этих «блоков» мы и получим.
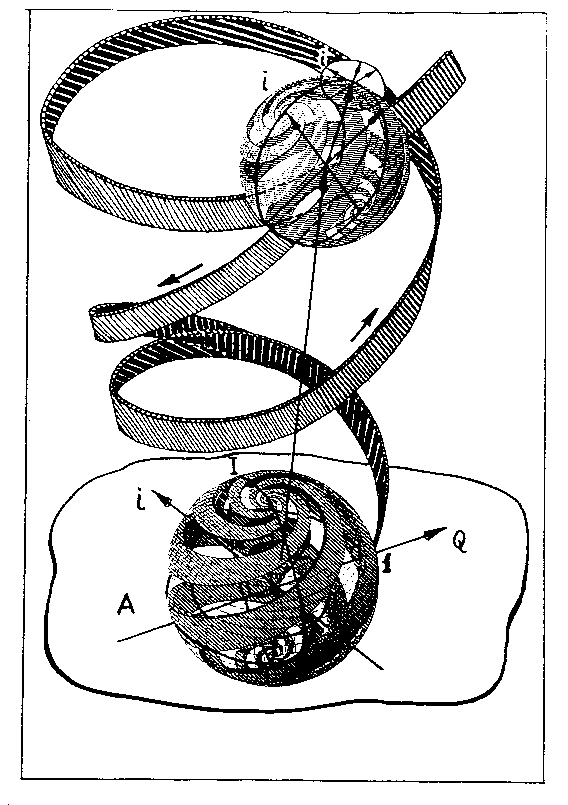
Рис.10. Пространство возведения в «мире октав»
Может быть множества Жюлиа, построенные в пространстве октав, будут еще более реалистичными биоморфами, ибо будут более расчленены на отдельные «органы» и «системы органов»?
Г. Галилей говорил, что книга природы написана на языке чисел – на языке геометрических фигур (для него это было одно и то же). Теорема Фробениуса ограничивает «нормальные числа» действительными, комплексными числами и кватернионами. Уже у октав появляется весьма странное свойство – несвязность (неассоциативность). А у еще более сложных чисел (Ок↑Ок = ?) появляются делители нуля – числа, отличные от нуля, произведение которых обращается в нуль (это значит, что конус возведения (см. рис.3) должен начинаться в нуле, чтобы одно из направлений, перпендикулярных плоскости А, делало модуль числа равным нулю). Т.е. чем сложнее (многомернее) становится число, тем менее оно похоже на привычные нам числа, тем больше в его поведении странностей и неожиданностей. Тем более похожи формы, порождаемые такими числами, когда на них накладывается некая динамика, на органические. Тем более у нас оснований смотреть на такие числа как на эйдосы природных форм, проявляемые потоком времени. Может быть именно так посмотрел на числа Велимир Хлебников, когда написал:
«Я взглянул на вас, числа, и увидел вас одетыми в звери...» (см. Рис.11, переводя взгляд снизу вверх – от «треугольников Галилея» до «зверей Хлебникова»).

Рис.11. Гравюра Маурица Эсхера.
|

